AEX

 

Terug naar index
21-04-2007
.
Een korte weekend update, en even vanaf de laptop, het is te mooi weer om binnen te zitten :-))
 
Hoewel men nog tot in de tijd van Columbus dacht dat de wereld plat was, vinden we in de boeken van Aristoteles rond 340 voor onze jaartelling al argumenten waarin deze aanvoerde waarom de aarde een bol moest zijn.
Hoewel men eerst dacht dat de aarde het centrum was waar alles omheen draaide ontdekte men later dat toch de zon het middelpunt is waar alles omheen draait.
Ptolemaeus ontwikkelde zelfs een model met de aarde als middelpunt waar de andere planeten in cirkelvormige banen omheen draaiden.
Het duurde tot rond 1514 voordat een Poolse priester Nikolaus Copernicus een ander model opstelde waarin de zon het middelpunt werd.
Omdat Copernicus er om een of andere reden waarde aan hechte dat zijn hoofd en romp één geheel bleven vormen, hield hij deze ontdekking lange tijd geheim om zodoende geen conflict met de kerk in die dagen te krijgen.
Daardoor duurde het nog bijna een eeuw voordat deze theorie door Johannes Kepler en Galileo Galilei in het openbaar werd gebracht.
Omdat men er vanuit ging dat een cirkel perfect is, en omdat men stelde dat het heelal perfect is, ging men er lange tijd vanuit de de planeten ook in een cirkel om de aarde, en later dan de zon zouden draaien.
Kepler echter verbeterde deze theorieën door te veronderstellen dat de planeten geen cirkelvormige maar ellipsvormige banen beschreven.
Het duurde vervolgens tot rond 1687 voordat er bewijs kwam van de ellipsvormige banen.
In dat jaar verscheen de “ Philosophiae Naturalis Principia Methematica” welke was geschreven door sir Isaac Newton.
Een van de belangrijkste dingen daarin was de vermelding van de zwaartekracht, de gravitatie.
Via zijn formules kon worden aangetoond dat deze kracht ervoor verantwoordelijk is dat planeten ellipsvormige banen beschrijven en geen cirkelvormige banen.
Hoewel later de relativiteitstheorie van Einstein aantoonde dat deze theorie niet geheel exact is, wordt deze theorie van Newton vanwege zijn eenvoud en maar geringe afwijking nog dagelijks toegepast.
Wat is nu het grote verschil tussen een cirkel en een ellips?
Een cirkel heeft één middelpunt waar omheen op gelijkmatige afstand ( de straal ) een lijn kan worden getrokken, een cirkel dus.
Ik zie dit middelpunt het zwaartepunt, als een krachtveld.
Meer over de cirkel vindt u op:  De cirkel is meer dan een rondje
Wat nu echter, wanneer we op hetzelfde moment niet met één krachtveld te maken hebben, maar met twee krachtvelden.
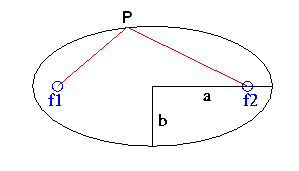
Figuur 1:
We zien in figuur 1 twee krachtvelden genaamd f1 en f2 welke invloed uitoefenen op punt P.
Punt P zal onder invloed van deze twee krachtvelden een ellipsvormige baan beschrijven.
Op Wikipedia is daar een leuke animatie van te zien:
Figuur 2:
De eigenschappen, de constructie enzovoorts behandelen we wel een keertje onder de kop basis wiskunde, maar ik wil er in dit geval nog wel even opwijzen, dat op het moment dat de punten f1 en f2 op elkaar komen te liggen dat er een cirkel ontstaat.
Ofwel, een cirkel is een ellips waarbij de krachtpunten f1 en f2 op elkaar liggen, in alle andere gevallen zal er een ellips te zien zijn.
In elke koersgrafiek zijn er ook punten te ontdekken waar de koers als het ware door wordt aangetrokken, ik noem dit zogenaamde krachtvelden.
Wanneer nu de koers erg dicht bij één krachtveld ligt, zal er een cirkelvormig gebied aanwezig zijn waarbinnen invloed wordt uitgeoefend op de koers, maar u kunt zich voorstellen dat wanneer er twee sterke krachtvelden aanwezig zijn en de koers zich ergens tussen deze twee krachtvelden bevindt, er een ellipsvormig gebied aanwezig zal zijn wat invloed uitoefent op de koers.
Omdat er meerdere krachtvelden in een koersgrafiek aanwezig zijn, zullen we deze ellipsen dus ook terug moeten kunnen vinden in een grafiek.
Laten we dit eens even controleren aan de hand van een grafiek van de AEX
Figuur 3:

 

U ziet het koersverloop vanaf 2000 t/m heden.
De daling vanaf het jaar 2000 tot Maart-2003 is weer te geven via twee grote ellipsen gemerkt A, welke gelijk zijn wat betreft afmetingen.
In het stijgende koersverloop vanaf maart-2003 tot en met heden zijn drie gelijke ellipsen getekend gemerkt B, met als achterliggende gedachte dat de ellipsen in deze stijgende golf waarschijnlijk gelijk zullen zijn, net als het geval was met de ellipsen in de dalende golf beweging.
Vanaf Maart-2003 ziet u ook een hele grote ellips, welke is berekend via een methode die ik zal behandelen zodra ik de ellips zelf behandel.
Wat opvalt, is dat deze ellips lijkt te eindigen in nagenoeg hetzelfde gebied als de laatste B -ellips, ondanks dat deze op een verschillende wijze zijn bepaald.
De kromme lijnen van de ellips zijn begrenzing lijnen, zeer belangrijk, ik kom daar bij de behandeling van de ellips dan ook op terug.
.
Omdat bijna alles wat groeit lijkt te voldoen aan de Fibonacci reeks, is het ook wel aardig om eens de Fibonacci spiraal in de grafiek te plaatsen.
Figuur 4:

 

Te zien is in figuur 4 dat telkens wanneer de koers de Fibonacci spiraal nadert, er eens koers reactie optreedt, en dat de koers momenteel nagenoeg de volgende lijn van de spiraal is genaderd.
.
Hieronder even een paar bekende grafieken, welke bijgewerkt zijn met de laatste koersdata.
Figuur 5:

De hoogste koers van vrijdag 20 April lag slechts twee punten verwijderd van de 1/3 SRL lijn, een Gann waarde.
Uit mijn stukjes over het "Square of nine" van Gann weten we dat deze waarde ook te bereken is op een andere wijze:   het kwadraat van( √217,8 + 8,5 )  --> 540,94
Gaan we uit van de slotkoers van 12-03-2003 dan wordt de berekening:  het kwadraat van( √218,44 + 8,5 ) --> 541,95
(540,94 + 541,95)/2 --> 541,4
.
Figuur 6:

Ondanks dat de getallen in het Murrey frame op een totaal andere wijze worden berekend, ziet u in deze grafiek ook de waarde van het ~540 gebied.
Let ook eens op hoe mooi de 7/8 lijn op afgelopen donderdag voor steun zorgde.
*
Bij verder stijgen zal het frame opschuiven, ofwel -- de koers gaat boven de 1/3 SRL-lijn uit waardoor deze aan de aantrekkingskracht van deze lijn ontsnapt -- ofwel de koers gaat door de Fibonacci spiraal lijn heen op weg naar de volgende -- ofwel de koers breekt uit de ellips op weg naar etc. etc.   ---- alles hangt aan elkaar.
*
Ook goed is in deze grafiek te zien dat de koers uitslag de laatste dagen in verhouding enorm is toegenomen, het ritme van lange stijgingen lijkt verstoord, iets wat men in de chaos -theorie "fibrilation" noemt, een wijziging in de frequentie, meestal gevolgd door chaos, ook daar zal ik eens een stukje over schrijven.
.
Figuur 7:

Zoals u weet zijn de rechte gekleurde lijnen Gann lijnen, getrokken vanuit Juni 2006, verder geen rekening houdend met het koers verloop; m.a.w. de lijnen zijn niet getrokken langs de toppen en dalen van het koersverloop
Zoals al wel eerder uitgelegd, zie ik de lijnen als een soort van aantrekkende krachtlijnen waar de koers moeilijk van los kan komen, maar zodra de koers er van los weet te komen, zal deze op weg gaan naar de volgende lijn om bij nadering daarvan door deze lijn te worden ingevangen.
In figuur 7 zien we dan ook dat het de koers nog steeds niet gelukt is om los te komen van de gele 2X1 lijn.
Afgelopen donderdag leek het bij opening er even op dat dit zou gebeuren, maar de koers opende op de grijze wusk lijn, keek er even onder, vond steun op de Murrey 7/8 lijn en sloot weer in de buurt van de gele 2X1 lijn, nog steeds in het aantrekking gebied van deze lijn.
Vrijdag keek de koers weer aan de bovenzijde van de gele 2X1 lijn en kwam in de buurt van de gele wusk lijn.
Zoals verwacht verwacht ik een grote beweging zodra de koers weet los te komen van de gele 2X1 lijn, of zodra deze de gele wusk lijn nadert.
.
Figuur 8:

Deze grafiek heb ik onlangs nog besproken, dus ik wil daar kort over zijn, u ziet het belang van kruisende Gann lijnen, horizontaal en verticaal, hoewel slechts de horizontale lijnen zijn ingetekend.
.
Figuur 9:

In bovenstaande weekgrafiek, ziet een stijgende koers van de AEX index, echter de oscillatoren welke eronder staan weergegeven geven allen aan dat er geen kracht achter de koers stijging zit, waardoor de kans groot is dat de koers zal draaien, duidelijk is de negatieve divergentie te zien.
.
Ook op dagbasis zie we dit verschijnsel, hoewel de RSI-14  in dat tijdframe de boel voor de gek houdt. Ik heb dat in de stukjes over de RSI-14  al vaker aangegeven, en dat is dan ook de reden waarom er altijd een controlerende oscillator moet worden gebruikt.
Daggrafiek AEX met oscillatoren:
Figuur 10:

Deze grafiek kent u ook al, dus we kunnen er kort over zijn.
Door de onderste oscillatoren wordt al langere tijd divergentie met de koers aangegeven, wat erop duidt dat de signalen van de RSI-14 niet geheel betrouwbaar zijn.
De RSI-14 was afgelopen vrijdag niet in staat om de snelle koersstijging te volgen wat op die korte termijn een negatieve divergentie tot gevolg heeft, maar die negatieve divergentie wordt onmiddellijk weer www
uitgenomen indien de koers maandag verder zou stijgen.
.
Veel wijsheid toegewenst,
Vriendelijke groet,
Jan.
.
Email: -->  Jan@JSTAS.com
.
Terug naar index
Disclaimer: Bovenstaande zijn slechts ideeën, verwachtingen en hersenspinsels. Ze hoeven dan ook helemaal niet te kloppen met de werkelijkheid. Handelen met deze gegevens op de beurs is derhalve voor eigen risico, en wordt afgeraden. U kunt daarbij al uw geld verliezen, en meer dan dat !!