07-01-2015
In de technische analyse op beurskoersen hebben we als basis de waarden van de koers -candle en het volume.
Op deze vijf gegevens (Opening -koers, Hoogste -koers, Laagste -koers, Slot -koers en Volume) laten we de indicator(en) los aan de hand waarvan we bepaalde signalen willen zien of filteren. Je zou denken dat daar niet zoveel mis kan gaan, je bepaalt welk signaal je wilt zien of filteren, je kiest vervolgens de indicator die dit kan en past bij de fase waarin het Fonds of Index verkeerd, je selecteert de juiste instelling .... ét voilá ... de signalen rollen over je scherm.
In de golf beweging van de grafiek zijn er echter componenten aanwezig die je in eerste instantie wellicht niet ziet, maar die er wel voor kunnen zorgen dat je indicator een output te zien geeft die er helemaal niet is! Dit kan zelfs als resultaat hebben dat je bij bepaalde instellingen van de gebruikte indicator handelt op zelf geproduceerde ruis in plaats van op gegevens uit de koersgrafiek.
En daarover gaat nu het volgende stukje, ik zal proberen uit te leggen wat er zoal mis kan gaan en nog belangrijker ... wat we daartegen kunnen doen.
Wie wel eens een Western heeft gezien zal opgevallen zijn dat de wielen van een koets soms achteruit lijken te draaien terwijl de koets vooruit rijdt. Wat gaat hier mis denkt u wellicht op zo’n moment. Het antwoord is snel te vinden wanneer we een blik in de digitale techniek werpen.
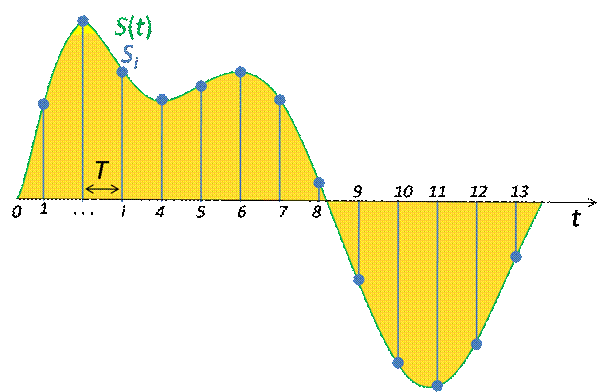
Wanneer we de analoge weergave van een golfvorm bekijken dan ziet u bijvoorbeeld het volgende plaatje (afkomstig vanaf Wikipedia.nl).
Figuur 1:

Op de horizontale as ziet u de tijd weergegeven, en de verticale as stelt de amplitude (waarde) voor.
Beurskoersen kunnen ook op deze wijze worden weergegeven, alleen zal de waarde (amplitude) dan normaliter boven 0 liggen.
Wanneer we dit signaal digitaal willen opslaan, dat moeten we op tijdstip t1 de waarde meten en die kunnen we dan vastleggen, vervolgens voor tijdstip t2 enzovoorts.
De ruimte tussen elk tijdstip ligt in dit geval vast, we noemen dat tijd-discreet.
We noemen het opslaan van de waarde op een bepaald tijdstip: bemonsteren (sampling), en het aantal monsters per seconde noemen we de bemonsteringsfrequentie.
Frequentie en tijd zijn omgekeerd evenredig; Frequentie = 1 /Tijd
Wanneer we dan later deze digitale gegevens weer om willen zetten naar een analoge weergave dan hoeven we slechts steeds bij elk tijdstip de juiste waarde weer te geven en er een lijntje tussen te trekken.
Duidelijk mag zijn, dat des te korter tijdstip T in bovenstaande figuur is, des te nauwkeuriger later weer de analoge waarden kunnen worden terug gezet.
Immers wanneer we slechts die punten zouden meten zoals in bovenstaande figuur is weergegeven, dan zullen bij reproductie diverse rondingen worden vervangen door een recht lijnstukje.
Dus des te meer meetpunten (een kleinere T dus hogere bemonstering frequentie) des te nauwkeuriger de reproductie weer mogelijk is.
Maar, waar ligt nu de grens?
Gelukkig hebben ‘knappe koppen’ dit al voor ons uitgerekend en dat leverde het beroemde ‘sampling theorema’ van Shannon op wat luidt:
“Een analoog signaal dat componenten bevat tot en met een maximale frequentie van f1-Hz, kan volledig worden gerepresenteerd door samples op gelijke onderlinge afstand (tijd-discreet) wanneer de sample-frequentie ten minste 2*f1 samples per seconde bedraagt.” (Frequentie --> f1 = 1 / T)
Dus een signaal van 3000 Hz zal met een frequentie van 6000 Hz moeten worden bemonsterd (gedigitaliseerd) om weer vanuit dat digitale signaal een goede reconstructie te krijgen.
Dat is dus 2 samples per periode van de hoogst gemeten aanwezige frequentie in het analoge signaal.
Dit is wel een ideaal beeld, omdat in de praktijk de benodigde filter technieken nooit 100% ideaal zijn, moet op een wat hogere frequentie worden bemonsterd, waarover later.
Wat gaat er nu eigenlijk fout bij een verkeerde bemonsteringsfrequentie (sample-frequency)?
We moeten dan iets verder in de formule duiken.
Het tijd interval T in figuur 1 kunnen we voor het bovengenoemde theorema weergeven als:
T = 1/(2*f1)
De maximale analoge frequentie f1 volgt dan door de formule anders neer te schrijven:
f1 = 1/2T in Hz.
In radialen: omega1 = 2*pi*f1 = pi/T rad/sec
Knappe koppen hebben dit verder uitgewerkt, en dan blijkt dat reconstructie na digitalisering van het analoge signaal ervoor zorgt dat het originele signaal zich herhaalt rond veelvouden van de bemonstering frequentie (+ en - omega).
Hoe ziet dat er in de dagelijkse praktijk uit.
Figuur a:
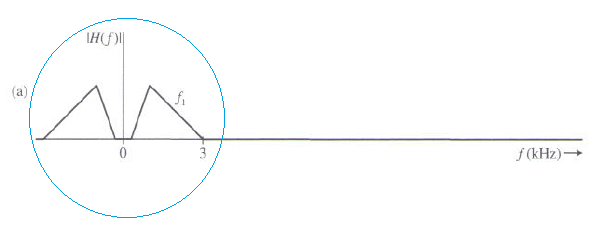
In figuur a ziet u een signaal met een maximale frequentie (horizontale as) van 3-kHz (3000-Hz).
Wanneer we dit signaal nu gaan bemonsteren met een frequentie van 8-kHz dan ziet het signaal er na reconstructie uit als figuur b.
Figuur b:
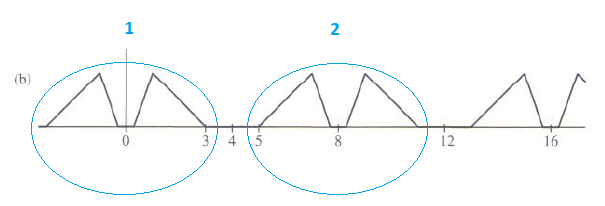
U ziet dat er boven de frequentie van 3 kHz ineens diverse signalen bij zijn gekomen.
Het originele signaal 1 ziet u herhaalt weergegeven als 2 rondom de bemonsteringsfrequentie van 8-Khz.
Dat is in de praktijk eenvoudig weg te filteren, we laten het signaal na reconstructie door een filter lopen wat alles boven de 5-kHz weg filtert.
We hebben hierboven gesampled met een frequentie van 8-Khz.
Het theorema zegt echter dat een sampling met de dubbele frequentie al genoeg is, dus 6-kHz zou moeten volstaan voor een signaal met als hoogste frequentie 3-kHz.
U ziet de weergave hiervan in figuur c.
Figuur c:
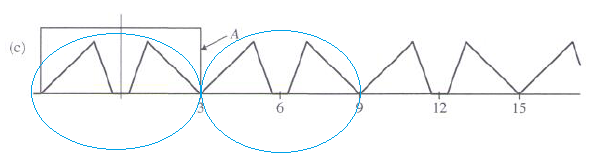
Op papier verloopt alles gladjes, we zien een herhaling van het signaal rond 6 kHz, dus niks aan de hand, we hoeven slechts het signaal boven de 3-kHz weg te filteren om de ongewenste herhalingen weg te werken.
Daarbij treedt er echter een probleem op, het is in de praktijk namelijk niet mogelijk een filter te construeren wat oneindig scherp afsnijdt bij 3-kHz (wat dus alles onder de 3-kHz doorlaat en net boven de 3-kHz niet).
Vandaar dat er moet worden gesampled op een hogere frequentie dan tweemaal f1 waardoor er een ruimte ontstaat die nodig is omdat een filter nu eenmaal niet 100% ideaal is (zie grafiek 2 en 3 verderop in dit verhaal).
Laten we eens kijken wat er gebeurt wanneer we bemonsteren op een lagere frequentie dan de frequentie die is voorgeschreven door het theorema van Shannon.
Laten we eens bemonsteren met een frequentie van 5-kHz in plaats van 6-kHz.
U kan al wel bedenken wat er gebeurt, immers het oorspronkelijke signaal zal zich nu herhalen rondom die 5-kHz, en dus interfereren met het oorspronkelijke signaal.
U ziet dit in onderstaande figuur d.
Figuur d:
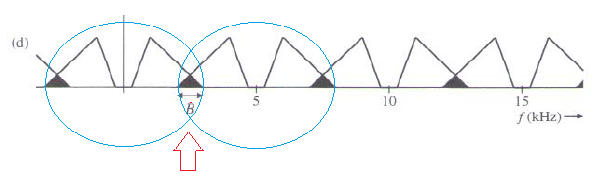
U ziet nu dat het oorspronkelijke signaal gedeeltelijk wordt overschreven door de opvolgende herhalingen in het spectrum.
Dit is een fout die niet meer kan worden hersteld, een verkeerde sampling frequentie geeft een vervorming die er voor zorgt dat het signaal er na reconstructie anders uitziet dan wat het was voor het proces.
Dit is dan ook exact wat er optreedt in die Western in het begin van dit verhaaltje, de te lage sampling frequentie ten opzichte van de draaiende wielen met hun spaken erin (een te laag aantal beeldjes per seconde van het opname apparaat) veroorzaken een fout die daarna niet mee te herstellen is, je kan daardoor aan de draairichting van het wiel niet meer bepalen in welke richting de koets rijdt.
Deze fout vanwege een verkeerde bemonstering frequentie wordt vouwvervorming genoemd, en een mooi Engels woord daarvoor is: Aliasing.
Mooi man, maar wat heeft dat nu te maken met onze beurskoersen? ;)
Wel, wellicht meer dan u denkt, en ik grijp daarvoor even terug op het werk van John Ehlers.
John Ehlers is een elektrotechnisch ingenieur die zich onder andere heeft verdiept in digitale filtertechnieken, en deze toepasselijk heeft gemaakt voor gebruik in onze technische analyse.
In één van zijn publicaties laat hij de volgende grafiek zien:
Grafiek 1:
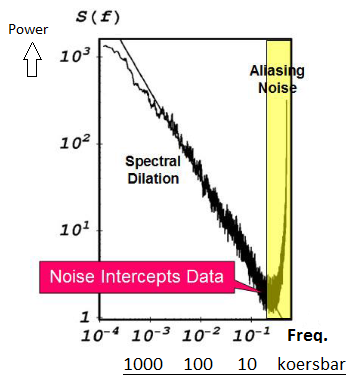
Op de horizontale as van deze grafiek ziet u de frequentie en op de verticale as het vermogen in een bepaalde golfbeweging weergegeven.
Ik heb onder de horizontale frequentie as even een schaal weergegeven met het aantal koersbars zoals we dat in onze grafieken gebruiken, dat zijn dus het aantal koersbars waarop u een indicator instelt.
In het geel gekleurde gedeelte ziet u de aliasing weergegeven, uw weet nu dat dit de vouw -vervorming is.
Bij hoger wordende frequentie ziet u dat de aliasing het oorspronkelijke signaal totaal overtreft in waarde. Of anders neergeschreven, onder een 10-koersbar periode wordt het oorspronkelijke signaal volledig overstemd door de aliasing.
Er treedt nog een ander verschijnsel op en John Ehlers noemt dit ‘Spectral Dilation’.
Bi lagere frequenties dan 0,1 dus bij meer dan 10 koersbars neemt het vermogen in de golf beweging toe met 6-dB per octaaf.
Deze ongewenste effecten willen we verwijderen en daarvoor kunnen we gebruik maken van filters.
*
In de technische analyse op koersgrafieken wordt als filter veel gebruik gemaakt van een gemiddelde, zoals een gewoon gemiddelde (SMA), een gewogen gemiddelde (WMA) en een exponentieel gemiddelde (EMA).
Ik heb daar al eens een stukje over geschreven wat u kan vinden onder de link: http://www.jstas.com/Gemiddelden/middelen_maar.htm
Ik raadt u echt aan bovenstaande link even serieus door te lezen, u leert dan iets over filteren.
Nu zijn de hierboven genoemde gemiddelden niet de beste filters. Om een behoorlijke demping van ongewenste signalen te verkrijgen moet er vaak met een lange periode instelling worden gewerkt wat dan weer een grote ‘lag’ tot gevolg heeft, de indicator loopt dan erg achter op de beurskoersen, je signalen komen te laat.
*
Laten we beginnen met het filter voor het zo goed mogelijk onderdrukken van het aliasing effect.
Uit bovenstaande stukje weet u dat dit inhoudt dat hogere frequenties moeten worden onderdrukt, ofwel onder de 10 koersbars.
Laten we eerst eens de demping bekijken van een 10 bar EMA wat we hiervoor zouden kunnen gebruiken.
Ehlers geeft de volgende grafiek voor de filterende werking van een 10 koersbar EMA.
Grafiek 2:
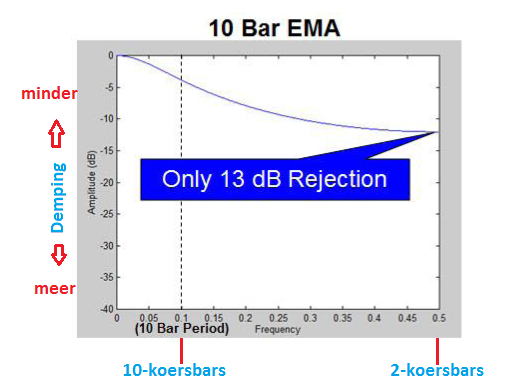
U ziet dat op de Niquist frequency (2 koersbars) de demping van de EMA 10 slechts 13 dB is.
Door nu gebruik te maken van filter technieken vanuit de digitale filter techniek kunnen we filters ontwerpen en gebruiken die ten eerste van een hogere orde zijn en ten tweede veel minder lag hebben.
De orde van een filter wordt bepaalt door de mate van verzwakking per octaaf.
Een eerste orde filter verzwakt 6-dB per octaaf.
Een tweede orde filter verzwakt 12-dB per octaaf.
Een derde orde filter verzwakt 18-dB per octaaf, en zo verder.
De demping eigenschappen van zo'n hoger orde filter van 10 bar geeft Ehler in onderstaande grafiek.
Grafiek 3:
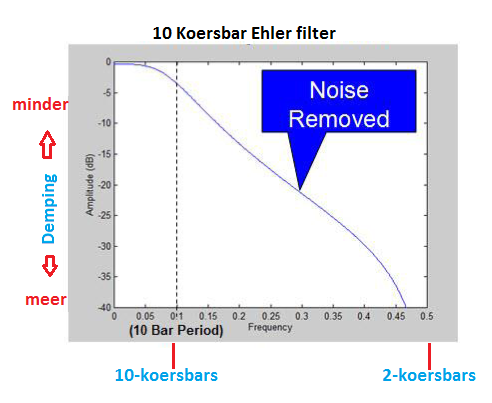
U ziet een enorm verbeterde demping terwijl de lag lager ligt dan van een EMA filter (het bewijs daarvoor laat ik nu achterwege, bij tijd in een ander werkstukje).
Wat u in grafiek 3 ziet is de demping van een hoger orde filter dan het EMA filter welke we verkregen hebben vanuit de digitale technieken.
*
Mooi voor zover, de foute analyse ten gevolge van aliasing kunnen we op deze wijze met het Ehler filter wegwerken, maar hoe gaan we te werk met die ‘spectral dilation’?
*
Voor de onderdrukking van ‘Spectral Dilation’ moeten we de langere golflengten onderdrukken, lagere frequenties dus.
De tools uit onze standaard gereedschapkist voldoen daar helaas ook niet.
De meeste tools hiervoor (oscillators en detrenders) acteren als een filter van de eerste orde, dus een demping van 6-dB per octaaf.
Maar, zoals ik al eerder in dit stukje beschreef, de ‘Spectral Delation’ neemt toe met 6-dB per octaaf. Wanneer we dan ter onderdrukking Oscillatoren of Detrenders toepassen die maar 6-dB per octaaf verzwakken is het gevolg hiervan is, dat lagere golflengtes niet uitgefilterd worden, behalve een beetje egalisering van de koersbeweging doen ze niet veel.
Pas wanneer we een hoger orde filter gebruiken ontstaat er resultaat.
Een tweede orde filter zal 12-dB per octaaf verzwakken, en dat zal dan wel een onderdrukking geven voor de ‘Spectral Delation’.
Een bijkomend effect is een ijkpunt voor de oscillator waarover wellicht meer een andere keer.
*
Oké Jan , tot zover .. effe samenvatten graag!
Ik heb proberen aan te geven tegen welke problemen je zoal aanloopt bij analyse van data, in dit geval de koers van een fonds of index etc.
Ik heb even de aandacht gevestigd op twee problemen, en dat is ‘Aliasing’ en ‘Spectral Dilation’.
Het ‘Alising’ effect kunnen we wegwerken door koersbars minder dan 10 (hogere frequenties) weg te filteren.
De ‘Spectral Dilation’ treedt op bij lagere frequenties (hoger aantal koersbars- zie grafiek 1) en die kunnen we uitfilteren door middel van een ‘HighPass filter’.
Samenvattend -kort door de bocht- om de aanwezige Aliasing en Spectral Dilation weg te werken moeten we aan de bovenzijde en aan de onderzijde van het frequentie spectrum filteren, en zo’n combinatie filter wordt een band-doorlaat-filter (roofing filter) genoemd.
U begrijpt nu al wel dat het roofing filter in dit geval dusdanig berekend moet worden dat alleen die frequenties moeten worden doorgelaten welke overeenkomen met een gebied wat ligt tussen de 10 en 48 koersbars. Deze 10 en 48 koersbars zijn gegeven door Ehlers, ik zal t.z.t. een stukje programma schrijven waarin u zelf deze waarden kan aanpassen.
Buiten deze bandbreedte wordt het te meten signaal weggedrukt door aan de ene kant ‘aliasing’ en aan de andere kant ‘spectral dilation’; buiten deze bandbreedte handelt u op –ruis-.
*
Jan, wanneer ik je dus goed begrijp moeten we een HighPass filter gebruiken om de 'Spectral Dilation' te verwijderen en een lowpass filter gebruiken om de Aliasing te verwijderen, alvorens we de data gaan gebruiken voor verdere analyse.
Ja helemaal goed, maar dan ben je er nog niet wanneer je bovenstaande allemaal goed gelezen en begrepen hebt ;)
Je zag bij het stukje over vouwfrequenties namelijk dat bij reproductie het signaal zich herhaalt rondom de sample frequentie.
Die herhaalde signalen willen we niet (we willen alleen het origineel) dus we moeten nog een lowpass filter plaatsen nadat het signaal bewerkt is.
Schematisch (verkort) ziet dat er als volgt uit.
Figuur 2:
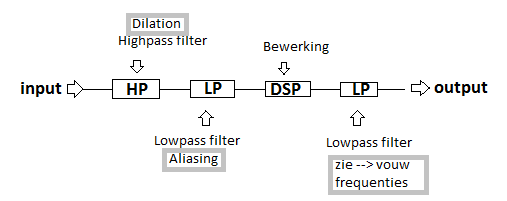
Het te bewerken signaal gaat eerst door een hoog doorlaatfilter, daarna door een laag doorlaatfilter die samen een band -doorlaat filter vormen.
Daarna vindt de bewerking plaats (DSP=Digital Signal Processing) waarna het bewerkte signaal nogmaals door een laag doorlaat filter gaat om alleen het gewenste signaal over te houden en niet de herhaalde reproducties rondom de sampling frequentie (zie een stukje terug in dit werkstukje) die laatste worden dus uitgefilterd.
Allemaal mooi man ;) maar wat kunnen we ermee in de dagelijkse praktijk, dat is immers wat telt!
Ja, wat kan je ermee, ten eerste is het misschien leerzaam om te weten dat wat je denkt te zien er misschien helemaal niet is; denk aan de terug draaiende wielen in de Western terwijl de koers vooruit gaat; wil je daarop handelen ?.. wil je handelen op de terug draaiende wielen van de beurs terwijl de koers de andere kant op gaat?
*
U weet nu het volgende:
Al heel snel, voordat u het door heeft, handelt u op ruis die ontstaat door een verkeerde aanpak.
Wanneer u geen weet heeft van Aliasing, zit u voordat u het beseft te handelen in de foute gegevens, ik noem dat maar even ruis.
Wanneer u geen weet heeft van 'Spectral Dilation' ,wel dan handelt u op deze spookverschijnselen.
En weet je wat je dan als gevolg daarvan vaak hoort in de markt: --> technische analyse werkt niet meer vandaag de dag!
*
Ik laat nu hieronder even twee grafieken zien met daarin de StochasticsK, dat is een stukje van de Stochastics zoals in de regel wordt gebruikt.
De Stochastics indicator valt onder de groep -oscillatoren-.
Oscillatoren moeten bij juist gebruik de trend uitfilteren en de cyclus weergeven.
Laten we even kijken naar die StochasticsK voordat we de filters inschakelen.
In mijn stukje TA-script code kan u die op vier manieren laten berekenen, maar ik pak nu even de meest gebruikte methode, en dat is een berekening op de H-L-C-koersen en dat dan met een periode van 20.
De ta-script-code vindt onder deze link: http://www.ta-script.com/forum/viewtopic.php?f=2&t=546&p=8525#p8525
Daar rolt de volgende grafiek uit.
Grafiek 4:
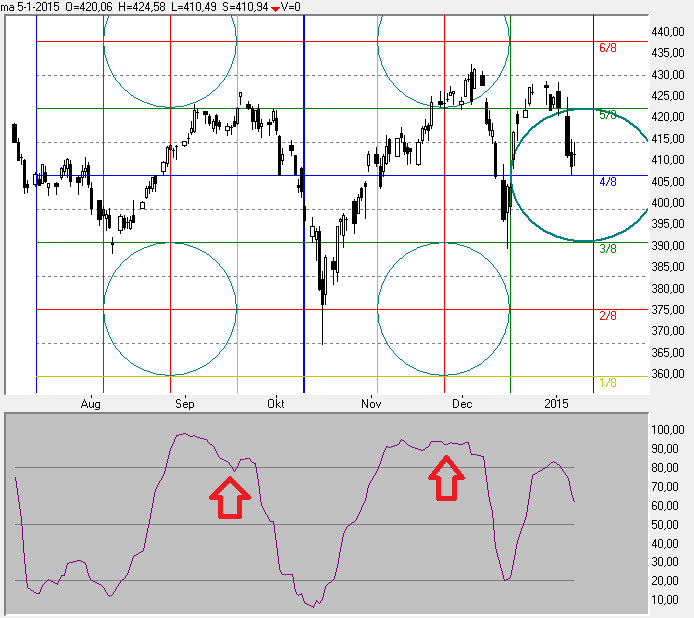
De ideale oscillator heeft een beweging van 0 - 100, maar wanneer dat niet volledig wordt gerealiseerd is dat geen probleem, ik wijs er alleen even op.
In grafiek 4 zien we wel een ander probleem, en dat is dat wanneer de koers omhoog blijft gaan (nadat een sinusvorm verloop eigenlijk alweer omlaag wil gaan) de oscillator bovenin blijft hangen; ik heb er even een paar pijltjes bij geplaatst. Dit 'hooghouden' van de indicatorlijn wordt veroorzaakt door wat Ehlers noemt 'Spectral Dilation'.
Wanneer we een oscillator hebben die daar geen last van heeft, zal deze theoretisch beter de cyclus aangeven.
Ik plaats daarvoor nu even hieronder ter vergelijk hetzelfde stukje koersgrafiek maar dan met de StochasticsK berekening na toepassing van de filters.
Grafiek 5:
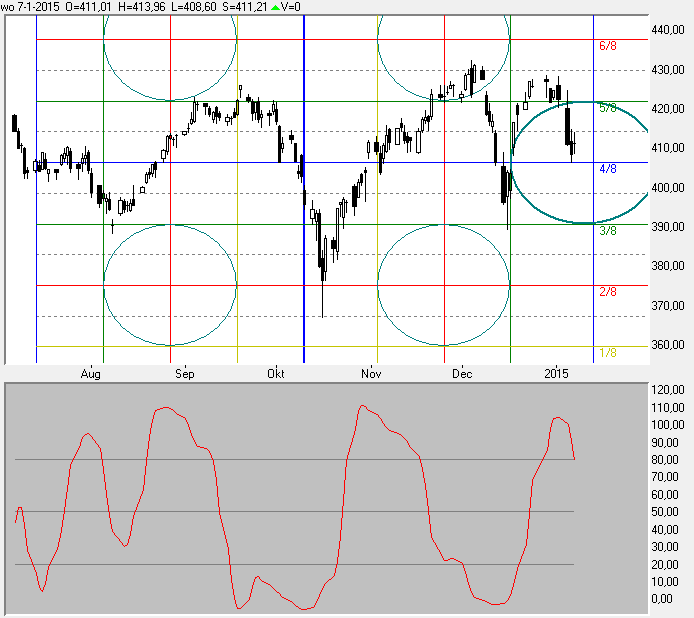
U ziet dat na de filtering de StochasticsK meer een sinusvorm verloop gaat krijgen, hij volgt meer de onderliggende cyclus in de koersgrafiek.
Het horizontale verloop wat u zag in grafiek 4 op bij de twee pijltjes is verdwenen doordat de 'Spectral Dilation' is verwijderd door het filter.
Ook beweegt de oscillator nu beter tussen 0 en 100.
Doordat nu beter de cyclus van de koersgrafiek wordt opgevolgd wordt dit door Ehlers een 'predictive' indicator genoemd.
Hiervoor gelden echter wel andere handel regels dan bij de traditionele Stochastics, maar ik wil het voor nu echter hier even bij laten wellicht een volgende keer.
---Het is niet slim om in een western de rijrichting van de koets te bepalen aan de hand van draairichting van de wielen --- doe dat dan ook niet met de beurskoersen .... ;-)
Vriendelijke groet,
Jan ;)
*************************************************************************************************************************************************************